新QC７つ道具（New Seven basic tools of quality）について

新QC７つ道具の概要

新QC７つ道具とは

新QC7つ道具とは、品質管理（Quality Control）で用いられる7つの手法のことです。
「N7」と略されて呼ばれることもあります。

従来のQC7つ道具は、主に数値データを扱うため、数値化が難しい問題や課題に適用できない弱点がありました。
新QC7つ道具では、主に言語データという定性的なデータを扱うため、製造業のみならず企画・設計・営業など様々な部門での活用できます。

新QC7つ道具は、以下の７つの手法となります。

親和図法
連関図法
系統図法
マトリックス図法
アローダイヤグラム法
PDPC法
マトリックスデータ解析法

新QC７つ道具の手法

親和図法（Affinity Diagram Method）

親和図法とは、言語データを親和性によって整理統合しながら問題解決する手法です。
親和性とは、物事を組み合わせたときの相性のよさ、結びつきやすい性質、という意味です。
つまり、雑多な事象に対して、共通事項や上位概念でまとめて整理していくと、ある種のまとまりや方向性があることに気づきます。
これを基に問題の構造や本質を見つけ出し、解決の糸口を探ることが親和図法の方法論です。

親和図法は「KJ法（文化人類学者である川喜多二郎氏が考案した手法）」が起源となっているといわれています。

連関図法（Relations Diagram Method）

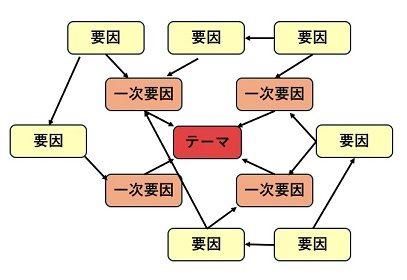
連関図法とは、複雑に絡み合っている事象について、因果関係のある要因を矢線で結び、相互の関連性を明確にすることで問題解決する手法です。
原因と結果、目的と手段などの相関について、それぞれの因果関係を「連関図」に整理して、分析を進めていきます。
連関図法は、要因を深堀りすることで根源的な要因に辿り着くことを目的としています。

連関図の作成手順は以下の通りです。

解決したい問題やテーマを決める。
問題に直接関係する要因（一次要因）３～５個程度を洗い出す。
二次要因から一次要因に向かって関係性を表す矢印を書きます。
要因の要因（二次要因）を洗い出し、必要に応じて三次要因、四次要因まで深堀りする
要因同士の関係性を矢印で結ぶ
根源的な要因を特定する。

系統図法（Tree Diagram Method）

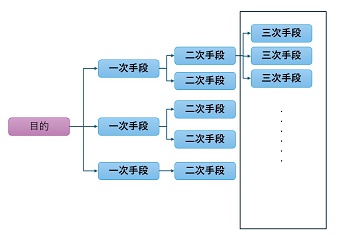
系統図とは、目的を達成するための手段や対策を系統的に展開して、最適な手段を見つけ出す手法です。
系統図を作成して可視化することで新たな視点と発想が得られ、最適な手段を見つけることができるようになります。

系統図は、簡単にいえば「なぜなぜ分析」を分かりやすく図式化した手法といえます。
目的を細分化しつつ、詳細化していき、具体的な解決法を探索します。

系統図の作成手順は以下の通りです。

達成したい目的を決める。
一次手段を２～５つほど検討します。
例えば、4M（Man＝人・Machine＝機械・Material＝材料・Method＝方法）に分けることは有効です。
二次手段以降（三次、場合によっては四次まで）を検討します。
具体的に行動できるレベルまで落とし込みます。
目的達成のためにやるべきことを選択します。

マトリックス図法（Matrix Diagram Method）

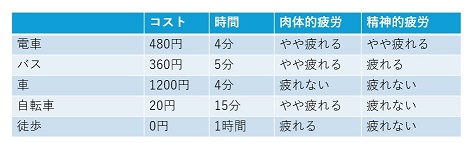
マトリックス図法とは、問題に関連する２つの要素を組み合わせて考えることにより、現状把握や課題の考察を見出す手法です。
マトリックス図を作成することで問題と対策案を可視化し、それぞれの対策案の効果と優先順位を決められるようになります。
系統図法と共に用いられることも多く、系統図法で導き出した対策案に対して、優先順位を決定することに役立ちます。

マトリックス図の作成手順は以下の通りです。
なお、マトリックス図の種類には、利用頻度の高いL型マトリックス図以外にも、T型・Y型・C型・X型などがあります。

解決したい課題を決める。
行と列に配置する要素を決める。
課題に対して、どのような要素を用いるかで、分析の精度が大きく変わるので注意が必要です。
一般的には、行には課題を、列には関係する要因を当てはめることが多いです。
行と列に配置する評価項目を記入する。
交点に対して関係性や評価を書き込む。
点数や評価から、判断を得る。

アローダイヤグラム法（Arrow Diagram Method）

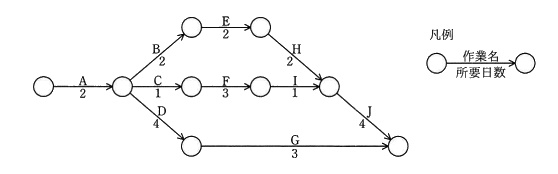
アローダイアグラム法とは、個々の作業を矢印で表して、作業同士を丸印で結ぶことで作業順序や依存関係を表現する図法です。
詳細はプロジェクトスケジュールネットワーク図を参照ください。

PDPC法（Process Decision Program Chart Method）

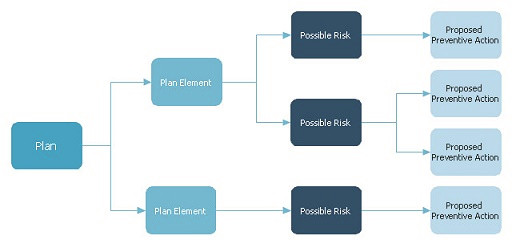
PDPC法とは、目的を達成するまでに想定される障害とその回避方法を図示して、事前に障害を回避するための策を講じておく計画立案手法です。
想定される状況を事前に整理して、フローチャート（プロセス決定計画図、過程決定計画図と呼ばれる）を作成して可視化します。
この図を用いることで、実際に問題が起こった場合に、迅速に適切に対応することができます。

PDPC法には次の2種類があります。

種類	説明
強制連結型	初期の計画時から、起こりうる不測事態を想定して、対応策を考える方法です。つまり、ルートをゴールに必ず結びつける方法です。
逐次展開型	計画を進めて、不測の事態が発生した都度打開策を考え、逐次追加補正しながら計画を修正する方法です。事前の計画ルートから外れても、新たなルートを作成して、ゴールに到達できるルートを探ります。

マトリックスデータ解析法（Matrix Data Analysis）

マトリックス・データ解析法とは、数値データをマトリックス形式（行と列の構成）に配置して、その特徴をまとめる解析手法です。
つまり、マトリックス図の列（または行）をできるだけ少ない項目数となる項目に置き換えて、データを整理しやすくする手法です。
マトリックスデータ解析法は、マトリックス図を見やすくして、データの特徴や傾向を捉えやすくすることで、俯瞰的な結論を得ることができます。

マトリックスデータ解析法では、項目数をまとめる際に、情報の損失を最小限にする工夫が必要となります。
そこで、「主成分分析」と呼ばれる手法を用います。
主成分分析は、マトリックス形式で集められた多くの数値データを、二次元平面図（Ｘ－Ｙ平面図）である散布図に表わし、異なる評価指標の座標軸からデータ相関をわかりやすく視覚化して示す手法です。