音楽理論_音律
音律とは
音律とは
音律とは、1オクターブの中での音程の並べる方法をいいます。
つまり、ある基準の音に対する音の高さ(音程)の相互関係を音律といいます。
より簡単に言い換えると、音律とはチューニング方法のことです。
例えば、ラの音(440Hz)を基準とした場合に、ドやソなどの音はどれくらいの高さに設定するかというルールが音律です。
音律の歴史について
西洋音楽における音律は、紀元前500年頃に発明されたピタゴラス音律から始まったと言われています。
この音律は、16世紀頃までは最もポピュラーな音律として使われ続けました。
しかし、オクターブが微妙にずれたり、3度の音がハモらないなど様々な不都合があったため、別の音律が提案されるようになりました。
15世紀〜16世紀(中世からルネサンス時代)には、和音の響きを美しくするために、純正律やミーントーン(中全音律)が考案されました。
さらに、18世紀にはあらゆる調に対応する調律として、ウェル・テンペラメントなどの音律が考案されてきました。
その後、19世紀後半に平均律(等分平均律)が普及し、これが20世紀において最も利用される音律となっています。
ドレミファソラシドの音階
ドレミファソラシドの音階を考案したのは、イタリアの修道士・音楽教師であったグイード・ダレッツォ(990年-1050年)といわれています。
ピタゴラスによって1オクターブを7つに分割する理論が確立されて以来、ピタゴラス音律(教会旋法)がグレゴリオ聖歌として伝承されました。
グイードは、グレゴリオ聖歌を教唱するために、洗礼者ヨハネ賛歌の歌詞の冒頭の音を、ut(ド)、re、mi、fa、sol、laとして音階の階名に利用しました。
これがドレミファソラシの音階を確立したきっかけといわれています。
※グイードは楽譜記譜法の原型を開発したことでも有名です。
ピタゴラス音律(Pythagorean tuning)
ピタゴラス音律とは
ピタゴラス音律とは、音階の全ての音と音程を周波数比3:2の純正な完全五度に基づいて導出する音律です。
古代ギリシアの哲学者・科学者であるピタゴラスが、モノコード(弦を張った楽器)を使った実験によって、弦の長さの比率が音程に影響することを発見しました。
さらに、「1:2」や「3:2」などの単純な比率で表すことが出来る音程は協和度が高いことを発見しました。
これらの発見を基に音程を構築して、考案された音律がピタゴラス音律です。
ピタゴラス音律の仕組み
ピタゴラス音律は、5度を基準で積み上げて考える音律です。
音程を積み上げるルールは以下の2点です。
・基準音から3:2の比率を積算する。
・オクターブを下げる場合には1/2を積算する。
具体的に各音の周波数を計算してみます。
まず、基準音(ラ音)を440Hzとしてチューニングします。
次に、ラ音から完全5度上の音は「ミ音」なのでこの音の周波数を計算します。
440Hz × 1.5 = 660Hz
660Hz × 1.5 = 990Hz
990Hz ÷ 2 = 495Hz
5度を積み上げていくことで、A→E→B→F# ... →G→Dと12音階を作成します。
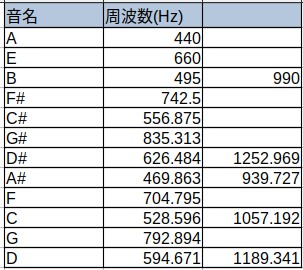
最終的に並び替えると以下のようになります。
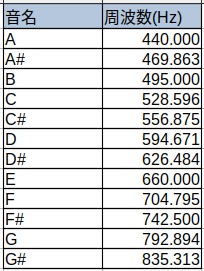
ピタゴラスコンマ(Pythagorean comma)について
ピタゴラスコンマとは、基準音と1オクターブ上の基準音で発生する誤差のことです。
例えば、A=440Hzを基準としてピタゴラス音律を構成した場合、D=594.671Hzの完全5度上の音は1オクターブ上のAとなります。
しかし、その値は「892.0065」となり、正しい1オクターブ上の「A=880Hz」と若干の差が発生します。
これは、音の比率が完璧に一致することが無いために発生する現象です。
ウルフの5度(Wolf interval)について
ウルフとは、ひどいうなりを持つ音程のことを指し、その不協和音が狼の吠声に例えられたものです。
ピタゴラス音律を無理やりに1オクターブ内に配置する場合、いずれかの完全5度をずらす必要があります。
しかし、このずらされた完全5度は、その狭い音程によって音楽的な不協和音を引き起こします。
これをウルフの5度といいます。
純正律(Just intonation)
純正律とは
純正律とは、音楽の音程(音高の間の距離)を、簡単な整数比で表現できる音律です。
具体的には、完全5度(例えばドとソ)の周波数比が2:3、長3度(例えばドとミ)の周波数比が4:5となるように調整された音律のことです。
この音律は、和音の響きを美しく、澄んだものにするとされています。
純正律の仕組み
純正律による長調(メジャー調)は、純正完全5度 (3/2) と純正長3度 (5/4) を用いて音階を定めます。
基準音からの比率は以下の通りです。

純正律による短調(マイナー調)は、純正完全5度 (3/2) と純正短3度 (6/5)を用いて音階を定めます。
基準音からの比率は以下の通りです。

シントニックコンマ(syntonic comma)について
シントニックコンマとは、完全5度を積み重ねた時(ピタゴラス音律)の長3度と純正3度との間で発生する誤差のことです。
この現象はピタゴラスコンマと同じく、音のうなり(ウルフ)を発生させてしまいます。
この音程を含む和音は非常に響きが悪くなり、そのため純正律では転調や移調が困難となります。
純正律のメリット
純正律のメリットは、倍音との不協和音がない、純正な和音が得られることです。
特に、三和音は4:5:6という単純な整数比で構成され、美しい響きになります。
純正律のデメリット
純正律のデメリットは、転調が難しいことです。
純正律は、特定の調においてのみ美しい和音が得られるように設計されています。
そのため、基準とした調以外に転調や移調すると、シントニックコンマの存在により音程が狂い、不協和音になりやすい傾向があります。
また、純正律は和音の響きを重視するため、旋律を演奏すると、音程のずれが目立ち、不均一な印象を与えることもあります。
純正律は、和音の美しさに重点が置かれているため、旋律では各音間の音程が不均等に感じられ、聴き心地が良くない場合があります。
平均律(12等分平均律)
平均律とは
平均律とは、1オクターブ内の音の高さを12に等分割し、それを半音と定義した音律です。
これはピアノやギターなどの現在広く使われている楽器で用いられている音律です。
A(440Hz)から始まる1オクターブ上がるまでの周波数は以下のようになります。
A : 440.00Hz
A♯/B♭ : 466.16Hz
B : 493.88Hz
C : 523.25Hz
C♯/D♭ : 554.36Hz
D : 587.32Hz
D♯/E♭ : 622.25Hz
E : 659.25Hz
F : 698.45Hz
F♯/G♭ : 739.98Hz
G : 783.99Hz
G♯/A♭ : 830.60Hz
A : 880.00Hz
平均律のメリット
平均律のメリットは、どんな調でも演奏しやすいということです。
転調しても大きな違和感もなく、自然に聞こえます。
これにより、多様な音楽表現が可能になりました。
平均律のデメリット
平均律は、純正律に比べて、音程のズレが生じやすいデメリットがあります。
特に、純正な和音を重視する音楽(例えば、管楽器やオーケストラのアンサンブル)では、不協和感が生じやすいという問題があります。
また、平均律では、特定の楽器(オルガンや管楽器など)で響きが不快になることがあります。
これは、平均律は完全1度と完全8度を除き純正な音程にならないため、わずかな誤差によるうなりが生じることが原因です。
※平均律でのうなりは、楽器の種類や演奏の仕方によって、それぞれ感じられる程度が異なるので、工夫で対処できる場合もあります。
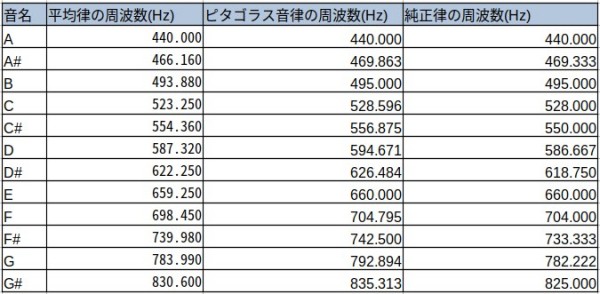
平均律と他音律の比較
平均律の周波数とピタゴラス音律、純正律の周波数を比較すると下記のようになります。